Petits jeux harmoniques

Depuis le temps que je parle d'harmoniques et que je promets d'y consacrer un article, il serait peut-être temps de tenir ma promesse ...

Observé par René Descarte et surtout décrit par Marin Mersenne dans son Harmonie universelle (1636), le phénomène des harmoniques (ou partiels) fut scientifiquement expliqué et appliqué par Joseph Sauveur à la composition des jeux d'orgues en 1702. C'est Jean-Baptiste Joseph Fourier qui, par un théorème célèbre, en a fait la démonstration mathématique en 1822. Jean-Philippe Rameau fut le premier à invoquer la série des harmoniques (Génération harmonique, 1737), pour justifier la théorie de l'accord parfait majeur.

La première notion importante ici est celle de son pur et de son complexe. Voici pour commencer une petite expérience réalisée à l'aide d'un diapason à branches en acier, accordé sur le La 440 Hz (La₃ dans la nomenclature latine, A₄ dans la nomenclature anglo-saxonne). Employé seul, le diapason est assez peu audible, car sa surface de contact avec l'air est réduite. Dans le fichier audio ci-dessous, le diapason est d'abord mis en vibration en le cognant contre un objet dur, puis (vers 0:09) le manche du diapason est appuyé contre la touche d'un dulcimer, tout près du chevalet.

On entend clairement la différence de timbre entre les deux sons. Le timbre est une signature sonore qui fait qu'on reconnaît parfaitement à l'oreille l'instrument sur lequel est jouée une note. Plus à ce sujet en fin d'article. D'autre part, le son est significativement amplifié par le dulcimer.

Rappel : En aucun cas je ne prétends faire un cours ou donner des leçons à qui que ce soit. Cette série d'articles sur la théorie musicale n'est qu'une mise au propre de mes notes personnelles sur le sujet. Merci de me signaler toute erreur, omission ou imprécision qui pourrait choquer le lecteur.

La figure ci-dessous est un sonogramme réalisé sur tablette avec l'application SpectrumView. Les fréquences sont portées en hertz (Hz) en ordonnées (axe vertical - Frequency) et le temps en secondes (s) en abscisses (axe horizontal - Time). L'amplitude sonore est représentée par une échelle de couleurs qui va du bleu pour la plus faible au rouge/orange pour la plus forte, en passant par le vert et le jaune :

Comme indiqué, la partie gauche de la figure correspond au sonogramme du diapason seul. On entend au début un bref bruit d'attaque correspondant au choc initial du diapason pour le mettre en vibration, puis un son aigu relativement bref, correspondant vraisemblablement à la trace sonore à 2640 Hz, en haut de la figure, qui disparaît très vite. A la suite de quoi le son se stabilise sur le La 440 Hz, jusqu'à l'extinction de la vibration. Une légère trace est visible à 880 Hz, qui disparaît également assez vite. Sur le reste du temps, le son du diapason peut être considéré comme un son pur. L'amplitude sonore est relativement faible.

Posé sur le dulcimer après avoir été remis en vibration (partie doite de la figure ci-dessus), le diapason produit toujours la vibration de 440 Hz, mais on observe en plus une trace à 880 Hz bien plus intense et durable qu'avec le diapason seul. D'autres faibles traces fugaces sont aussi visibles au dessus, vers 1320 et 1760 Hz, qui n'étaient pas détectées avec le diapason seul. Le son du diapason posé sur le dulcimer est un son complexe, formé d'au moins deux vibrations, de 400 et 880 Hz.

On est en droit de se demander d'où provient la différence entre les deux expériences. Elle vient bien sûr de la caisse de résonance du dulcimer. Les vibrations du diapason éveillent d'autres vibrations dans le bois et/ou l'air de l'instrument, et ce sont ces dernières vibrations que l'on perçoit plus intensément. L'instrument entre en résonance avec le diapason. Il se met lui-même à vibrer aux mêmes fréquences ou à des fréquences très proches et, comme sa surface est plus grande au contact de l'air, le son est amplifié. Contrairement à un ampli électronique, le dulcimer n'utilise pas d'énergie extérieure (électrique, par exemple) pour augmenter le signal. C'est une amplification acoustique où l'énergie initiale donnée par le choc du diapason sur un objet dur est sensiblement la même, mais le rendement de conversion de cette énergie en vibrations de l'air est bien meilleur dans le cas du dulcimer.

La différence entre son pur et son complexe est peut-être encore plus nette sur le profil temporel de la figure suivante, qui montre la variation d'amplitude sonore (en ordonnées) en fonction du temps (en abscisses). Ces profils ont été obtenus avec le logiciel Audacity. Pour faciliter la comparaison, j'ai choisi des portions des tracés où les amplitudes sont sensiblement les mêmes, mais globalement, le son avec dulcimer est plus fort que le son sans dulcimer. Le son pur du diapason seul, en haut de la figure, est clairement une fonction sinusoïdale du temps :

C'est un phénomène périodique, qui se reproduit identique à lui même au bout d'une période T, ici égale à ≈ 2,27 millisecondes (1/440 Hz) [pour un rappel des définitions de fréquences, périodes et longueurs d'onde, voir Intervalles en fréquences du 03 mars 2018]. Lorsque le diapason est appuyé contre le dulcimer, le signal est également périodique, avec la même période de ≈ 2,27 ms, mais il n'est plus sinusoïdal. Le profil temporel est en fait la somme de deux sons purs interférents de fréquences f1 = 440 Hz et f2 = 880 Hz. C'est donc un son complexe.

On démontre que la période du son résultant d'une telle interférence est le PPCM (Plus Petit Commun Multiple) des périodes composantes. Un son pur de fréquence f2 = 880 Hz a une période T2 = 1/f2 (1/880 = 1, 136 ms). La période T de ≈ 2,27 ms pour le son résultant est bien le PPCM de 1,136 et 2,272. Le son (complexe) issu de cette interférence a exactement la même période, et donc la même fréquence, que le son (pur) le plus grave. C'est un La 440 Hz.

Tout le monde a vu, bien sûr, que le rapport 880/440 = 2/1 est le rapport des fréquences caractéristique de l'octave. Ceci explique pourquoi l'intervalle d'octave est si consonant: deux sons distants d'une octave donnent l'impression de n'en entendre qu'un (voir à ce sujet l'article Sur la corde du 06 février 2018).

Les notes produites par les cordes d'un dulcimer quand on les pince sont elles aussi des sons complexes. La figure ci-dessous montre à gauche les sonogrammes du La₂ (A₃ ≈ 220 Hz) et du Ré₃ (D₄ ≈ 294 Hz) produits respectivement par la corde médiane et la chanterelle libres (= non frettées, ou cordes à vide). Noter le grand nombre de fréquences composant chacun des deux sons :

La multitude des traces est frappante dans les deux cas. Encore plus remarquable est leur disposition régulière sur l'axe vertical des fréquences. Elle donne l'impression d'une échelle avec des barreaux régulièrement espacés, dont la durée de vie décroît à mesure qu'on y monte. Ce n'est d'ailleurs pas qu'une impression. Chacune des fréquences relevées pour ces sons qu'on appelle partiels est un multiple de la fréquence la plus basse, dite fondamentale. Quand il s'agit de multiples entiers de la fondamentale F (par ex. : 2*F, 3*F, 4*F ... etc.), on les désigne par le nom d'harmoniques. Cette situation existe pour la corde isolée, pour autant qu'on puisse entendre et analyser le son produit. Dans notre exemple, le son des cordes est passé au travers du filtre de la caisse de résonance de l'instrument, qui a pu amortir certaines fréquences (voir Au fil du bois du 18/09/2018), en amplifier d'autres, ou encore les déplacer légèrement, de sorte qu'elles ne sont plus exactement des multiples entiers de la fondamentale. Dans ce contexte, on préfère parler de partiels plutôt que d'harmoniques, mais le principe reste globalement le même.

Ce principe, c'est qu'une note de musique est constituée d'une fréquence fondamentale (symbolisée ici F), souvent la plus énergétique et la plus persistante au cours du temps, et de toute une série de fréquences secondaires qui viennent s'ajouter et se mêler à la première pour lui donner son timbre. Certaines ont plus d'énergie que d'autres et durent plus longtemps. C'est en partie par cette combinaison, ce cocktail de sons qu'on reconnaît l'instrument, qu'on distingue par exemple un La joué sur un piano d'un La joué sur une guitare ou un banjo. En un mot, qu'on identifie le timbre de l'instrument.

La partie droite de la figure ci-dessus montre les amplitudes (en décibels - dB - axe vertical) en fonction des fréquences. La tendance, déjà visible sur les sonogramme par la gamme des couleurs allant du bleu au rouge, est que l'amplitude décroît avec le numéro du partiel. Cette distribution des amplitudes et des durées de vie des partiels fait que seules les cinq ou six fréquences les plus basses contribuent réellement au son entendu.

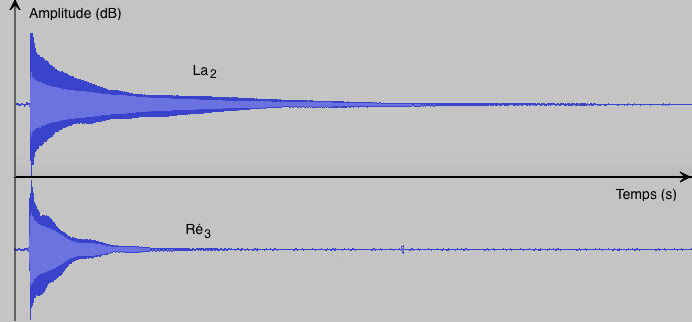
La différence de durée entre le La₂ de la corde médiane et le Ré₃ de la chanterelle se voit bien sur les profils temporels réalisés avec Audacity. Après une augmentation brutale d'amplitude au moment où on relâche la corde pincée au doigt (phase dite d'attaque; en anglais attack), les amplitudes des deux notes décroissent rapidement de façon quasi-exponentielle (phase dite de décroissance; decay en anglais), puis beaucoup plus lentement (phase dite d'entretien; sustain en anglais), avant de s'annuler complètement (phase d'extinction; release en anglais) :

La différence de durée des deux notes peut s'expliquer en partie par la nature des bois utilisés dans ce dulcimer. Le cerisier dont est fait la table d'harmonie est justement réputé pour facilter l'entretien des notes graves. La complexité des sons produits par le dulcimer se voit aussi sur des agrandissements de ces deux profils, au début de la phase d'entretien :

Dans tous les cas, la période (et donc la fréquence) du son résultant reste égale à celle de la fondamentale, selon le principe du PPCM, puisque toutes les fréquences partielles sont censées être des multiples de la fréquence fondamentale.

Mais d'où viennent ces partiels ou harmoniques qui accompagnent la fondamentale quand on pince une corde? La réponse est dans les modes propres de vibration des cordes, et le moment est venu de parler de l'incontournable expérience de Melde.

Franz Melde (1832-1901) était un physicien allemand connu pour ses travaux sur les ondes stationnaires produites sur une corde tendue, ce qui est aussi notre sujet d'étude du moment. Le principe de l'expérience est extrèmement simple: une corde est tendue entre deux points dont l'un est animé par un générateur de vibrations à fréquence variable :

Quand on allume le générateur de courant, la corde se met à vibrer à une fréquence X. C'est une oscillation forcée - une déformation de la corde se propage depuis le vibreur jusqu'à l'autre point d'attache d'où elle est renvoyée vers le vibreur etc. Ce vibreur génère donc un train d'ondes progressives qui se déplacent le long de la corde dans les deux sens :

Aux très basses fréquences le mouvement de la corde semble un peu anarchique, mais en augmentant progressivement la fréquence du vibreur on arrive à ceci: la corde forme un fuseau (on dit aussi un ventre) entre les deux points d'attache qu'on appelle nœuds :

C'est une onde stationnaire. Si on augmente encore la fréquence, on perd l'image du fuseau unique mais assez vite on arrive sur une image à deux fuseaux séparés par un nœud central (flèche) où la corde est immobile, comme d'ailleurs au point de fixation de droite :

Puis à trois fuseaux séparés par deux nœuds, etc. (en principe, jusqu'à l'infini et au delà...) :

Ces images sont extraites d'une vidéo pédagogique visible sur Youtube à cette adresse.

On l'aura deviné : les fréquences auxquelles apparaissent les fuseaux et les nœuds sont toutes des multiples entiers de la fréquence fondamentale (celle qui donne un fuseau unique).

Ces figures à 1, 2, 3, 4, 5, 6, etc... fuseaux représentent les modes propres de vibration de la corde. Ce sont donc les harmoniques de vibration de la corde. Comme on le sait depuis Mersenne et ses fameuses lois (voir Sur la corde du 06 février 2018), la fréquence fondamentale dépend, quand à elle, de la longueur de la corde, de sa tension et de sa masse linéique.

En résumé, quand on pince la corde d'un dulcimer, celle-ci se met simultanément à vibrer selon tous ces modes, produisant une série de fréquences inversement proportionnelles aux longueurs vibrantes : longueur totale de la corde pour le premier harmonique à un fuseau, demi-longueur pour le second harmonique à deux fuseaux, tiers de longueur pour le troisième harmonique à trois fuseaux, quart de longueur pour le quatrième harmonique, etc :

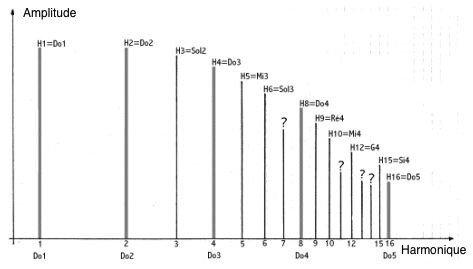
Selon ce principe, le premier harmonique (H1) correspond par définition à la fréquence fondamentale F de la corde entière. Le second harmonique (H2) a pour fréquence 2*F, c'est à dire qu'il correspond à l'octave supérieure de H1. En partant de Do₁ à 32,7 Hz, nous aurions Do₂ (65,4 Hz). Le troisième harmonique (H3) a pour fréquence 3*F et se place dans l'octave supérieure, entre H2 (2*F) et H4 (4*F). En partant de Do₁ ça serait Sol₃, avec une fréquence de 98,1 Hz. On pourrait le ramener dans l'octave de base, entre H1 et H2, en lui soustrayant une octave: 3*F ÷ 2/1 = 3F/2. En partant de Do₁ ça serait Sol₁ (49 Hz);  c'est bien sûr la quinte de Do₁ - on reconnaît le rapport superparticulier 3/2 caractéristique de la quinte.

Le cinquième harmonique (H5) se situe dans la troisième octave au dessus de H1, entre H4 et H8. En partant de Do₁ on aurait Mi₃ (163,5 Hz). On peut le ramener lui aussi dans la première octave en lui retirant, cette fois, deux octaves, ce qui donnerait 5F/4, avec un rapport superparticulier de 5/4, caractéristique de la tierce majeure.

Le sixième harmonique H6 a une fréquence double de celle de H3. On aurait Sol₃ (196,2 Hz) en partant de Do₁, à l'octave de Sol₂ déjà trouvé. A l'exception de H8 qui correspondrait à Do₄ (261,6 Hz), l'analyse des harmonique devient plus compliquée dans cette gamme de fréquences. De plus, beaucoup de ces harmoniques, surtout impaires, sont en dissonance plus ou moins forte avec la fondamentale. Heureusement pour nous, les harmoniques au dessus de H6 sont rarement audibles, car top faibles en amplitude ou de trop courte durée.

Alors. Maintenant que nous en savons un peu plus sur les harmoniques et les partiels, que pouvons nous en faire?

Les harmoniques permettent de décrire les modes de vibration d'une corde isolée. En principe, ils sont, par définition, plus élevés en fréquence que la vibration fondamentale et ajoutent de la clarté et du brillant (en anglais : clearness and brightness/brillance) pour reprendre les termes de Sir James Jeans dans son livre Science and Music de 1937. Par rapport à un son pur, comme celui du diapason par exemple, les harmoniques plus élevées en fréquence enrichissent la note fondamentale, lui donnant vie et intérêt.

Dès que la corde est mise en relation avec un système amplificateur, comme une caisse de résonance par exemple, les vibrations perdent une partie de leur caractère harmonique et sont appelées partiels. Les partiels participent pour une grande part au timbre de l'instrument, car le bois et l'air modifient les vibrations des cordes par leurs résonances propres.

Comme pour tout instrument à cordes pincées, il est possible de modifier le timbre d'un dulcimer en en pinçant les cordes en différents endroits. Mon système de mesure est trop imprécis pour aller plus en détail dans cette affaire, mais déjà, sur la figure ci-dessous (panneau de droite) on peut faire la différence entre une corde (ici la chanterelle à vide, accordée en Ré3) pincée en son milieu (= au niveau de la frette n°7 - A ) ou près du chevalet (= à l'extrémité de l'instrument, après le strum hollow - B) :

Selon la théorie, les partiels 2 et 4 devraient être complètement absents quand on pince la corde en son milieu, car alors on introduit un maximum de mouvement en un point de la corde où ces vibrations sont censées avoir un nœud immobile. J'observe bien en A un affaiblissement général des partiels pairs, en particulier 2 et 4, mais pas une disparition complète. Le son obtenu dans ces conditions est relativement chaud, plutôt doux et peu brillant, peut-être même un peu creux. Ces mêmes partiels pairs sont bien présents quand on pince la corde près du chevalet en B et on note également un peu plus d'énergie dans les partiels de plus hautes fréquences. En conséquence, le son est plus brillant, plus métallique, un peu plus "nasal", avec même une certaine dureté.

Un dernier point illustré par cette figure (panneau de gauche) concerne ce que j'appelle les harmoniques "de jeu", pour les différencier des harmoniques "des physiciens". Certains interprètes aiment terminer ou ponctuer un morceau avec quelques notes très "cristallines", qui font toujours leur petit effet. Pour obtenir ces notes, il faut pincer la corde avec le pouce de la main droite tout en maintenant l'index de la même main légèrement posé sur la corde au dessus d'une frette. C'est plus facile à faire au niveau de la frette n° 7 qui est, je le rappelle, au milieu de la VSL. Ecouter le fichier audio joué sur les trois cordes d'un dulcimer au niveau de la frette 7:

Dans la partie de gauche, le sonogramme précédent montre trois essais comparés au Ré₃ de la chanterelle à vide et au Ré₄ de la chanterelle frettée à la position 7. On note, au passage, que tous les partiels de Ré₄ trouvent une correspondance avec un partiel sur 2 (les numéros pairs) de Ré₃: 1' avec 2, 2' avec 4, 3' avec 6, etc. Pour le problème qui nous intéresse, il apparaît que les notes cristallines résultent d'une combinaison particulière de ces deux profils. Les partiels pairs y sont plus forts que dans le profil de Ré₃ et les partiels impairs y sont plus faibles que dans le profil de Ré₄.

Tout ce qui vient d'être dit s'applique aux vibrations transversales des cordes, c'est à dire des vibrations où chaque point d'une corde se déplace perpendiculairement à la direction de propagation de l'onde. C'est comme pour les rides qui se déplacent à la surface de l'eau autour du point de chute d'une goutte de pluie ou d'un petit caillou : chaque point de la surface monte et descend quand une ride passe à son niveau. En musique, les vibrations transversales sont les plus importantes, mais il faut savoir qu'il en existe d'autres, comme par exemple des vibrations longitudinales. Quand on tire sur la corde avec le doigt pour la pincer, elle s'allonge forcément un petit peu, pour revenir à sa longueur initiale quand on la lâche. Mais elle ne le fait pas immédiatement : elle se raccourcit en réaction à l'allongement de départ, mais un peu trop, de sorte qu'elle doit se rallonger un peu, et ainsi de suite, à la façon d'un ressort. Cette succession d'allongements/raccourcissements se fait aussi de façon périodique et déplace les points de la corde dans l'axe de celle-ci, c'est à dire longitudinalement. De plus, quand on pince la corde avec le doigt, elle a tendance à tourner sur elle-même, à se vriller dans un sens, pour tourner dans l'autre sens quand le doigt la lâche, en réaction, encore une fois dans un mouvement périodique à l'origine de vibrations radiales. Ces autres types de vibrations ont eux aussi leurs harmoniques. Il faut le savoir mais ne pas en faire un cauchemar, car on les entend finalement très peu.

Il y a en musique un nombre considérable d'applications du principe des harmoniques et des partiels. Chaque type d'instrument, qu'il soit à cordes où à vent, a des histoires à raconter là-dessus. Les quelques notions rappelées ici suffisent toutefois pour comprendre un certains nombre de détails techniques de lutherie, qui seront décrits ultérieurement.

A+